Differentiators

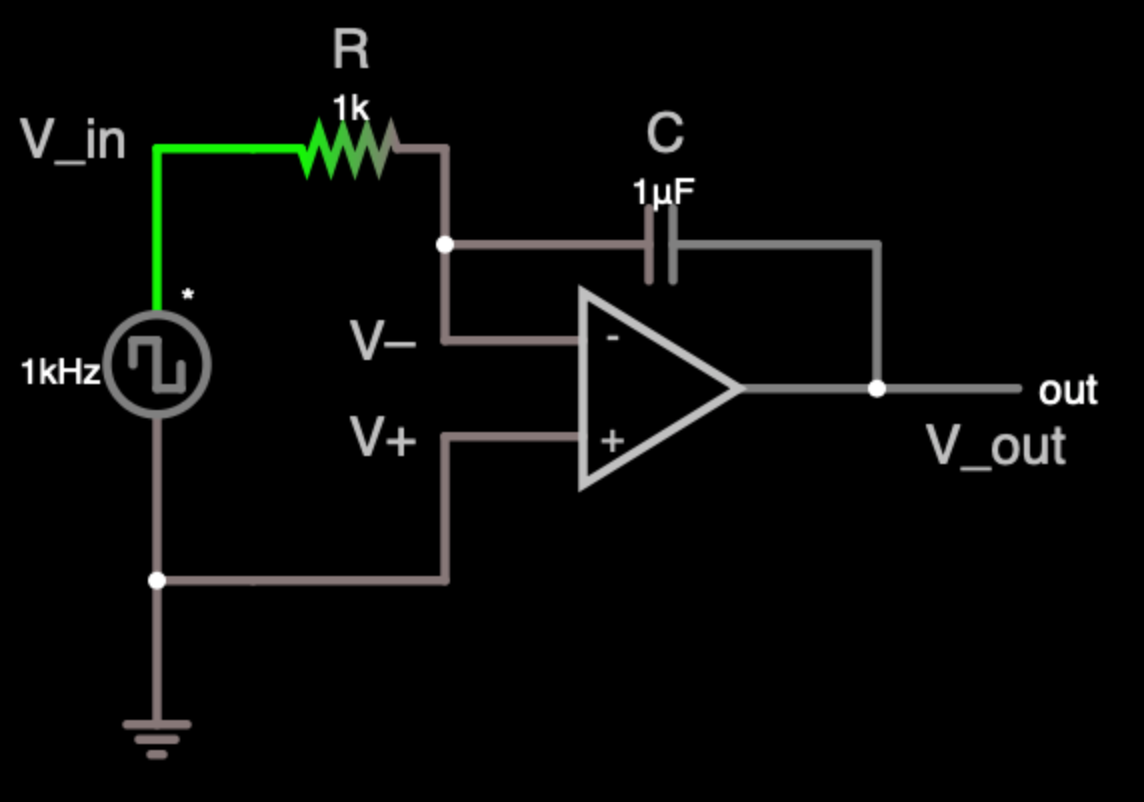
Simple passive RC or LR circuits can act as circuits that passively differentiate their input, i.e. \(V_{out} \propto \frac{dV_{in}}{dt}\), but op amp differentiators allow more control (with careful thought about the details of the circuit).

An ideal op amp has infinite input impedance and draws no current, so in the ideal simple circuit below, the current through the resistor and capacitor is:

\[I_C = C \frac{d\left(V^- -V_{in}\right)}{dt} = I_R = \frac{V_{out}-V^-}{R}\]

Assuming an ideal op amp, then for this circuit \(V^- = V^+ = 0\), so

\[C \frac{dV_{in}}{dt} = \frac{-V_{out}}{R}\]

\[\therefore V_{out} = - RC\frac{dV_{in}}{dt}\]

A Simple Op Amp Differentiating Circuit.

Build the above circuit on your breadboard, and play with various inputs and observe the outputs.

• You can use whichever op amp you prefer.
• Power your circuit from your DC power supply, using whichever outputs are appropriate..

Integrators

An ideal op amp has infinite input impedance and draws no current, so in the ideal simple circuit below, the current through the resistor and capacitor is:

\[I_R = \frac{V^- -V_{in}}{R} = I_C = C \frac{d\left(V_{out}-V^-\right)}{dt}\]

Assuming an ideal op amp, then for this circuit \(V^- = V^+ = 0\), so

\[\frac{-V_{in}}{R} = C \frac{dV_{out}}{dt}\]

\[\therefore \frac{dV_{out}}{dt} = -\frac{1}{RC}{V_{in}}\]

\[\therefore V_{out} (t) = -\frac{1}{RC}\int_0^t V_{in}(t')\,dt'\]

A Simple Op Amp Integrating Circuit.

Build the above circuit on your breadboard with Wavegen input, and play with various inputs and observe the outputs.

• Monitor the input and output with Scope channels 1 & 2 respectively.

The above simple integrator is not a practical circuit because it is sensitive to even tiny DC offsets on the input or non-zero currents flowing through the op amp. To improve the circuit we can try:

• shorting out any DC offset to ground at the input of the op amp, or
• shorting out any DC offset to ground at the output of the op amp, or
• adding DC feedback in parallel to the capacitor’s AC feedback, or
• blocking DC on the output.

Timer

The LM555CN is one of the family of 555 timer chips.

• See the lecture for more information on 555 timers and piezos.

Build the circuit in Figure 6-5 of the NE555P Spec Sheet, with nominal \(R_A=330k\), \(R_B=100k\), and \(C=47nF\).

• \(R_L\) can be left out, i.e \(R_L=\infty\)
• Measure the actual values of any resistors and capacitors before inserting them in your circuit.
• Duty cycle for a square wave is one of your scope measurement functions, which can save a bit of time.

Buzzer

Let’s expand the above circuit into a tunable, battery powered, push-button buzzer. Build this circuit.

A Simple piezo buzzer.

Notes:

• “R_fake” is not a real component to be included in your circuit. It is just avoid a “Capacitor loop with no resistance!” error in the simulation.
• If your simulation slows down when you push the switch, restarting the simulation with RUN/Stop should speed it back up.
• If you chose to use a low-power 6004 op amp for earlier exercises, make sure you do not accidentally put 9V into its power pins. It is only rated to 6V.
• Use a 9V Battery Snap Connector to connect to the 9V cell. (Negative terminal of the battery to Common, positive terminal to the circuit’s DC power.)

The piezo connector wires may be too soft to insert into the breadboard sockets, so you may want wrap them around some small jumper wires inserted in the sockets. (Soldering the wrapped joins would be best, but is probably not neccessary for this temporary circuit.)

Connect the piezo to the output and confirm that it buzzes when the button is pressed.

Replace one of the resistors with a 100k trim-pot, and confirm that the buzzer frequency changes as the trim-pot resistance is changed.

• Choose the resistor to replace based on getting the widest frequency range and better (i.e. closer to 50%) duty factor for better sound.