Rayleigh-Bénard and Bénard-Marangoni convection
If you take a horizontal fluid layer and maintain a temperature difference across it by heating from below and cooling from above, you will find that the fluid flows in a pattern of convection cells if the temperature difference exceeds a threshold value. The fluid motion transports additional heat over and above that carried by thermal conduction through the fluid. Many variations on this process have been studied in the laboratory since Bénard's first experiments around the turn of the century. The onset of convection is the archetypal example of a pattern forming instability.
This simplest and most studied version is Rayleigh-Bénard convection, shown schematically below.
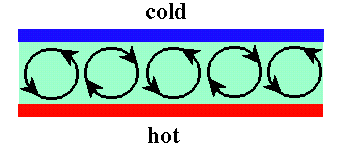
Here the fluid, shown in green, is confined between rigid plates which are held at constant temperature, with the hot plate below. In a classic 1916 paper, Lord Rayleigh showed that an initially motionless fluid layer becomes unstable to small flow perturbations when the temperature difference is sufficiently large. (Actually, Rayleigh fudged a bit on the boundary conditions, but this was patched up by Jeffreys in 1926). Flow perturbations grow when the buoyancy forces on a perturbed parcel of fluid become sufficient to overcome dissipation due to viscosity and thermal diffusion. Hot fluid near the bottom thermally expands and becomes lighter than the fluid above it, so it rises, cools and returns in an overturning flow. This motion is opposed by the viscosity of the fluid and the tendency of thermal diffusion to smooth out temperature gradients. The flow pattern consists of rolls or hexagonal cells, depending on the details of the temperature dependence of the fluid properties. The flow pattern may be stable, or it may fall prey to a host of secondary instabilities or become chaotic. For papers on some experiments on this system, see the Rayleigh-Bénard papers page.
Many early experiments used fluids heated from below with no confining plate on the top surface. In this arrangement, the top surface is free to move and deform. It was not realized until 1956 that this can lead to a second instability mechanism involving gradients in the surface tension, which in general coexists with Rayleigh's buoyancy mechanism, but dominates in thin layers. This situation, now called Bénard-Marangoni convection, is shown schematically below.
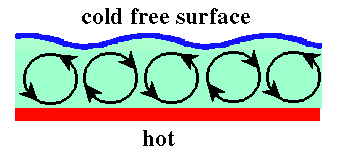
Here, a positive temperature fluctuation on the free surface leads to a local decrease in the surface tension, if the temperature derivative of the surface tension is negative. Gradients in the surface tension cause surface traction forces away from the warmer spot. These forces drive flows in the bulk of the layer and deform the surface. The flows in the bulk pump warm fluid up from the lower part of the layer, reinforcing the initial temperature fluctuation, leading to an instability and a flow which is driven by surface tension forces. In practical situations, the cooling of the top surface is often assisted by evaporation, for example in drying paint. This instability does not involve gravity, so may be expected even under zero-g conditions.
In any well-controlled experiment on Bénard-Marangoni convection, one must impose the temperature on the free surface by using a cooled rigid plate above it, with a layer of thermally conducting fluid in between, usually air. Inevitably, the upper fluid also partakes of some of the convective motion, and may even be Rayleigh unstable on its own. Theoretical treatments of the Bénard-Marangoni problem traditionally only consider the bottom fluid, subject to some assumptions about the boundary conditions at the free surface. A more physically correct and experimentally relevant approach is to consider two immiscible fluids with a deformable interface in between, in which the complete fluid mechanics of both layers is included. This situation is shown schematically below.
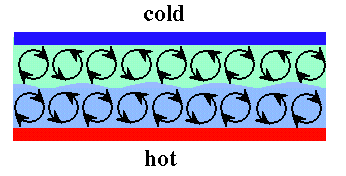
If the layers are thin enough, the resulting coupled convection may be driven mainly by surface tension gradients at the free surface, just as in the traditional Bénard-Marangoni case.
The Experimental Nonlinear Physics Group, Dept. of Physics, University of Toronto,