This One Goes To Eleven.

Researchers at the University of Toronto turn quantum interference up to a new level.

Two photons are better than one. Many of the most precise measurements in science and technology are based on interference, often interference of light waves. (In one form or another, this principle underlies technologies ranging from atomic clocks to radar speed guns to projects such as LIGO searching for gravitational waves.) An "interferometer" can easily be sensitive to position changes on the order of the wavelength of light, which is slightly less than a micron (one one-thousandth of a millimetre). But if every photon which goes through an interferometer can provide a position resolution on the order of a micron, scientists can make the measurement more precise by sending more photons through, just as Gallup can conduct a better poll if it interviews more people. Normally, every time you increase the number of photons (the intensity of the light) by a factor of 100, you improve your resolution by a factor of 10.

Several years ago, Jonathan Dowling and others noted that if a collection of photons were entangled according to the laws of quantum physics, rather than being sent through an interferometer independently, one could gain much more: increasing the photon number by 100 could in fact improve the resolution by 100. (A version of this idea called "spin squeezing" has now already been applied to improve the accuracy of some of the most precise clocks in existence.) At the time, however, no one knew how to entangle more than two photons in the right way. It was quickly shown that with two, the technique worked; soon thereafter, our group showed how this could be done with three, and several other groups pushed it to 4 and 5.

As usual, there was no free lunch. For the original proposal to work, all of the photons needed to reach the same detector at the end. And as the number of photons rose, such an event rapidly became less likely (exponentially less likely, to be precise). It started to seem as though even if physicists could one day learn to entangle 100 photons, the odds of them all reaching the same detector would be astronomically small, making the technique useless in practice.

In 2009, Mankei Tsang proposed a clever new variant of the technique. If detectors are placed at every position a photon could possibly reach, and every possible event is recorded (whether or not multiple photons hit the same detector), one can calculate the "centroid," or average position of all the detected photons. This can be done without having to discard any of the photons, unlike the original proposal. And Tsang showed that such centroid measurements would benefit from the same advantage as the earlier idea. Bob Boyd's group quickly verified the theory with two photons and two detectors. But of course, the interest of the proposal is that even as the number of photons and detectors grows, data should still be obtainable with good efficiency.

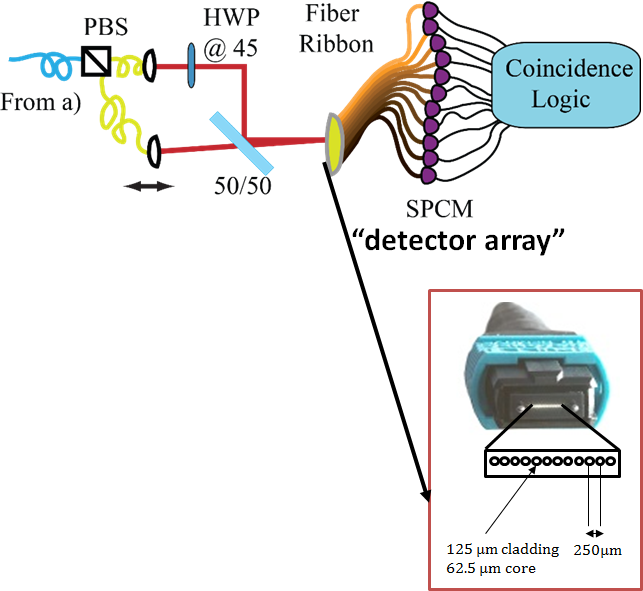
In the new work, we have used a "fibre ribbon" to collect photons and send them to an array of 11 single-photon detectors, which allowed us to collect nearly all of the multi-photon events. Sending independent photons or 2, 3, or 4 entangled photons into our interferometer, we saw clear evidence for the resolution advantage of entangled light. While two photons are better than one, eleven detectors are far better than two: this work opens up a path for using entangled states of light to carry out ultra-precise measurements.

Our technical article is: Lee Rozema, James Bateman, Dylan Mahler, Ryo Okamoto, Amir Feizpour, Alex Hayat, and Aephraim Steinberg, Scalable spatial superresolution using entangled photons, Phys. Rev. Lett. 112, 223602 (2014). [also available at http://xxx.lanl.gov/abs/1312.2012]

For Further Reading:
Advances in quantum metrology, Vittorio Giovannetti, Seth Lloyd, & Lorenzo Maccone, Nature Photonics 5, 222 (2011) [also available at http://xxx.lanl.gov/abs/1102.2318]
Quantum Imaging beyond the Diffraction Limit by Optical Centroid Measurements, Mankei Tsang, Phys. Rev. Lett. 102, 253601 (2009)
Quantum Interferometric Optical Lithography: Exploiting Entanglement to Beat the Diffraction Limit, Agedi Boto, Pieter Kok, Daniel Abrams, Samuel Braunstein, Colin Williams, and Jonathan Dowling, Phys. Rev. Lett. 85, 2733 (2000).

Back to Aephraim's home page