Magnetism arises from electron-electron interactions in a solid, and its manifestations range from ferromagnetism (which is seen in fridge magnets or your iPod), to more intricate forms of order such as antiferromagnetism which are harder to `see’. Most such forms of magnetism can be viewed as simple classical orders - they can be viewed, in a simple cartoon picture, as a state in which there is no `entanglement’ of the spin degrees of freedom on different sites. More delicate orders, which necessarily involve strong entanglement of spins on few or many sites, are often found in frustrated magnets - materials where either the geometry or the interactions prevent any simple `classical order’.

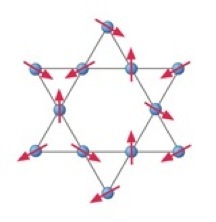
A prototypical example of strong frustration is illustrated in the above Kagome lattice model of spins where various local spin rearrangements exist which preserve the classical energy of the system leading to a large number of ground states. Another example which has been in the news a lot is `spin ice’ - an Ising model on the pyrochlore lattice which also has a large number of ground states. A study of such systems motivates a practical definition of `frustration’ as one where the classical version of the spin Hamiltonian allows for a large number of ground states, exponential in the number of spins in the system, which implies a residual entropy density in the classical model at zero temperature.
An interesting and challenging question in this field is to ask how quantum effects lift this classical degeneracy and lead to vanishing entropy density at T=0 in accordance with the third law of thermodynamics. The answer is that the system often ends up in interesting and new states of matter by forming delicate superpositions of the classically degenerate spin configurations, states which we are hard pressed to discuss using any simple `cartoon’ pictures, but which are nevertheless unique ground states of the quantum Hamiltonian. Motivated by trying to understand such theoretical questions and in order to address possible states which occur in a number of strongly correlated materials, we have studied several models of frustrated quantum magnets using a variety of theoretical approaches. A partial list of relevant publications is listed here, some of which was carried out in collaboration with my student Ganesh.
. Field induced Neel order of honeycomb quantum paramagnets (spin liquids, VBS
states and AKLT states
R. Ganesh, D. N. Sheng, Y. J. Kim, A. Paramekanti, arXiv:1012.0316
. Neel to Staggered Dimer transition in a honeycomb lattice JQ model
A. Banerjee, K. Damle, A. Paramekanti, arXiv:1012.4546
. Frustrated spirals and lattice nematic orders on the honeycomb lattice
A. Mulder, R. Ganesh, L. Capriotti, A. Paramekanti, Phys. Rev. B 81, 214419 (2010)
. Magnetic analog of supersolidity in the triangular lattice spin-1/2 XXZ mode
D. Heidarian, A. Paramekanti, Phys. Rev. Lett. 104, 015301 (2010)
. Gapless spin liquids on the 3D hyper-kagome lattice of Na4Ir3O8
M. Lawler, A. Paramekanti, Y.B. Kim, L. Balents, Phys. Rev. Lett. 101, 197202 (2008)
. SU(N) quantum spin models: A variational wavefunction study
-
A.Paramekanti, J. B. Marston, J. Phys. Cond. Matt. 19, 125215 (2007)
. Quantum paramagnetic ground states of the Heisenberg antiferromagnet on the star lattice
B. J. Yang, A. Paramekanti, Y. B. Kim, Phys. Rev. B 81, 134418 (2010)
. Spin liquid phase in a spin-1/2 quantum magnet on the kagome lattice
S. V. Isakov, Y. B. Kim, A. Paramekanti, Phys. Rev. Lett. 97, 207204 (2006)