ADVANCED UNDERGRADUATE LABORATORY
EXPERIMENT 32, FILM
Thin Film Interference
References updated by Barbara Chu, August 2006
Revision: March
2006 by Yi Chai
Original
By: Jason Harlow, 2006
1. Introduction
The
interference of reflected waves of light from transparent layers of material is
responsible for many beautiful phenomena in nature, such as butterfly wings,
peacock feathers and soap bubbles.
Multiple layers of thin transparent films with various indices of
refraction can be deposited on glass or metal substrates in a variety of ways
to control light. This has many
applications in science and industry, including anti-reflection coatings,
mirrors and optical filters.
Since
the discovery of the phenomenon of interference colors associated with thin
solid films, immense studies of the science and technology of thin film have
been conducted for nearly two centuries. Majority interest in this field has
been dominated by the unforeseen behaviors of solid films and the usefulness of
consequential optical properties with potential applications in mirrors and
interferometers. In particular, exploitation of the optical interference
phenomenon has led to development of instruments with tunable reflectance and
transmittance.
When thin film based mirrors are used for the purposes of
reflection and transmission, the most ideal system bears a minimized absorption
of incident light. Such systems are made possible by formation of non-metallic,
or dielectric, coated thin films, sometimes referred to as dielectric mirrors.
The process involves deposition of multilayer dielectric material onto glass
substrate. The choices of the type and thickness of the dielectric layers allow
for adjustable reflectance targeting at specific range of wavelengths. This
experiment carries out the fabrication of multilayer high reflectance
narrowband thin films by the photometric method.
2. Theory
To
investigate the optics of thin film interference, we will follow the derivation
of Fowles Chapter 4, and Hecht Chapter 9.
The general solution encompassing oblique incident light can be deduced
following the derivation of Chopra [2] page 722.
Single Layer Dielectric Thin Film
First consider the case of a single layer of dielectric
material, with thickness d and index
of refraction n, deposited onto a substrate
with index of refraction nS.
This sample is exposed to a medium with index of refraction n0, typically air. As shown
in Figure 1, when light of vacuum wavelength λ0 is normally incident on the sample, transmission
and reflection from both interfaces occur.
Figure 1. Electric and Magnetic fields across a single
dielectric layer
The boundary conditions
require that the electric and magnetic fields be continuous at both interfaces.
They yield the following equations:
First interface
(1)
(2)
Second interface
(3)
(4)
To get equations (2) and (4)
the relation 
was used. The phase
factors eikd and e-ikd in equations (3) and
(4) result from the fact that the wave has traveled a distance of d inside the dielectric layer; thus it
is advanced or delayed by a phase of kd,
where k is the wave number.
By eliminating the amplitudes within the layer, E1
and E’1, equations (1) through (4) can be combined to yield:
(5)
(6)
Equations (5) and (6) can be
represented by a matrix equation of the form:
(7)
In equations (7), r is called the reflection coefficient
with
and t is called the transmission coefficient with
finally, M is the transfer matrix and
(8)
Solving for r and t gives
(9)
(10)
As the result, the
measurement of the reflectance R and
the transmittance T are given by R=|r|2 and T=|t|2, respectively.
Physically, R and T indicate the proportion of light
intensity reflected by and transmitted through the dielectric system.
Question 2.1.
With 
, evaluate R and T for single layer dielectric films of
ZnS (n = 2.3) and MgF2 (n = 1.35). How do these values compare with
those of a bare glass substrate (for glass, n = 1.5)?
Question 2.2.
In general, for , what happens to R
and T if a single layer of thin film
on glass substrate exposed to air for:
i)
n
of dielectric greater than nS?
ii)
n
of dielectric larger than nS?
Substitute
some values of different dielectric materials and verify. Consult Chopra page
750 Table III for refractive indices of some common materials used in thin
film.
Question 2.3.
Repeat question 2.2 for 
and 
Multilayer All-dielectric Thin Film
Now consider the situation where there are N dielectric layers coated above the
substrate. The layers are labeled {1,
2, 3 … N}. They have indices
of refraction {n1, n2, n3 … nN}
and thicknesses {d1, d2, d3 … dN},
respectively. Similarly, the reflection and transmission coefficients of this
system are related by a matrix equation:
(11)
where Mi denotes the transfer matrix of the ith layer and the transfer
matrix Meffective is the
product of the transfer matrix of the various layers. All other properties
remain identical to the case of a single dielectric layer but making use of Meffective.
First consider a
double layer thin film composed of two dielectric materials, A and B. These two
adjacent layers have index of refraction nA
and
So the thickness of each layer can be calculated to be:
(12)
In this case, using equation (8) and (11), the transfer matrix is found
to be:
Now consider a stack of alternating layers of dielectric A
and dielectric B. If there are N pairs of such double layer dielectrics, the
transfer matrix becomes:
Substituting this result into equation (9) one can find the reflection
coefficient to be:
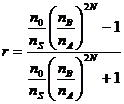
It is easy to verify that, with the increase of N, R approaches unity if nA and nB are different. Consequentially, a stack of
quarter-wavelength alternating dielectric layers forms a high-reflectance thin
film at a particular wavelength, λ0.
Question 2.4. How is the wave number k related to λ0?
Question 2.5. Verify that for quarter wavelength
thickness.
Question 2.6.
For an 8-layer high reflectance thin
film composed of alternating ZnS and MgF2 on glass substrate, sketch
a plot of the reflectance versus number of deposition layers, quantitatively
indicating the local minimums and maximums. How would the plot change if MgF2
is deposited first rather than ZnS? In either case, what is the net change of
reflectance? As you can see, even for small value of N, theory predicts a reflectance close to unity.
Question 2.7. A beam of white light falls at normal
incidence on a plate of glass of index n and thickness d. Show that minimum
reflectance occur at those wavelengths such that 
, where λ0
is the vacuum wavelength and N is an integer. This means that reflection and
transmission functions are periodic with respect to wavelength and this is
called a channeled spectrum.
Fabry-Perot Filter?
Description needed.
3. Deposition Technique
Operation under Vacuum
The multilayer thin film is to be fabricated under vacuum
in this experiment. Before beginning, read the write-up for the second-year
laboratory “Evaporation of Silver Films” for a thorough understanding of the
components of a vacuum system and the evaporation process. Do not worry about
the thickness estimation methods since a different one will be used. Become
familiar with the operation of the Edwards High Vacuum System used in this
experiment.
The Photometric Method
For dielectric films deposited on a transparent substrate
of a different refractive index (glass is used in this experiment), the optical
reflectance and transmittance behavior of the film-substrate combination, at
fixed wavelength of incident light, shows an oscillatory behavior as a function
of film thickness because of interference effects. Recall from question 2.2,
reflectance is reduced or enhanced depending on the relative values of
refractive indices of the film and the glass substrate.
The setup of photometric monitoring is summarized in the
diagram below, consult Chopra page 99 and explain the functionality of the
method.
Figure 2. The photometric monitoring setup.
In this setup, the reflected light passes by a bandpass
filter so that a short range of wavelength is monitored by the detector.
Question 3.1. How can one achieve the same
functionality without using a bandpass filter?
Question 3.2.
Use the spectroscopy described in section 4, measure the visible
wavelength range transmission spectrum of the filter used in the above setup.
How good is this filter?
Question 3.3.
What are some limitations to the photometric method? What happens with
increasing number of layers deposited?
Determining the film thickness
Film thickness is related to and can be determined from
the maxima and minima of the reflectance which occur at intervals given by (Chopra,
page 99)
[13]
where m is the order of the maximum or minimum and all other variables as
previously defined. The illustration below shows the observed variation of the
reflectance and transmittance of alternating ZnS and MgF2 quarter
wavelength films.
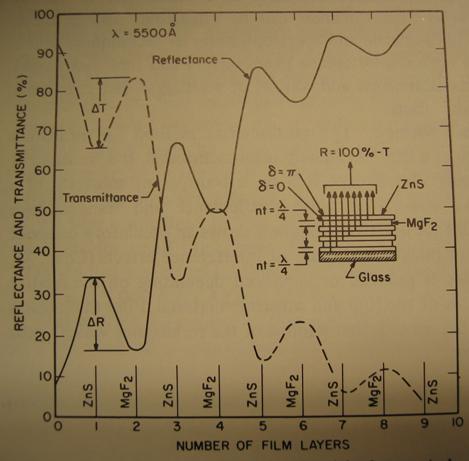
Figure 3. Reflectance and Transmittance of increasing number
of multilayers
Steckelmacher et al., Vacuum, 9:171
(1959)
Question 3.4.
Show that, after two maxima or minima are traversed (first being the
value at zero deposition), thickness for a single layer film is quarter
wavelength. (Hint: consider equation (12)).
Therefore by monitoring maxima and minima while depositing,
the thickness of each film is controlled to be quarter wavelength.
Question 3.5.
Calculate the actual thickness of quarter wavelength layers of ZnS, MgF2,
and cryolite (Na3AlF6) if blue light is monitored.
Question 3.6.
Make predictions to the shape of the channel spectrum with respect to
the filter used, indicating quantitatively the critical points.
3. Evaluating Optical Properties of Your Film
The
spectrometer consists of a wavelength dispersive device and a photomultiplier.
A prism is used to pick out photons of specified wavelength and transmit them
to the photomultiplier. A mechanical system of gears and springs attached to
the prism is adjusted to vary the specified wavelength. With your multilayer
thin film at the slit opening, obtain transmission spectra by scanning through
the visible wavelengths of light. (Hint: overlay the spectra on top of a white
light source spectrum for ease of comparison.)
The Photomultiplier
Photomultipliers are extremely sensitive detectors of
light, or photons. Incident photons strike the cathode material, and produce
electrons as the result of photoelectric effect. These electrons are
accelerated towards the electrode, while undergoing the process of secondary
emission. Secondary emission effectively
multiplies the electron signal. The electron multiplier consists of numerous
small electrodes called dynodes. Each dynode is held at a positive voltage with
respect to the previous one. When electrons leave the photocathode, they have
the energy of the incoming photon. While traveling towards the first dynode,
the electrons gain energy from the electric field. On arriving at the dynode
with much greater energy, the electrons can cause emission of low energy
electrons. The original electrons from the cathode, together with the newly
generated low energy electrons, then are accelerated toward the second dynode.
This process repeats and a cascading effect occurs, which result in a high
accumulation of charge arriving at the anode. This effect induces a sharp
noticeable current pulse in the device even if only a single photon enters the
cathode.
Measure the channel spectrum of your multilayer thin film
in the visible wavelength.
Question 4.1.
Compare and contrast the measured channel spectrum with respect to
theoretical predictions.
Question 4.2.
How does the slit width of the spectrometer affect the shape of your
spectra? What is a suitable slit width to yield a representative spectrum?
Question 4.3.
With a narrow slit width (approximately 1000 µm), take spectra of your
thin film at different positions on the thin film. Does this have an effect on
the shape on the channel spectrum? If so, is it understandable? What part of
the experiment most likely resulted in such changes in the channel spectrum?
Question 4.4.
How would incident light at different angles affect the channel
spectrum?
Some Discussion Questions
1.
What is a
Fabry-Perot Filter? Describe its functionality and composition
2.
Why might one
wish to use MgF2 instead of cryolite in making thin films with ZnS?
3.
How does the
addition of a silver deposition layer on top of the multilayer high reflectance
thin film affect its performance? You may wish to add a silver deposition layer
and contrast the channel spectrum from before and after.
4.
In an one-way
mirror, the metallic/dielectric coatings on the surface of glass substrate
actually result in a so called “half-layer” thin film. This just means that
neither of transmittance nor reflectance is very high or very low. Then how
does an one-way mirror work? (Hint: think about the slit width and the white
light source in the spectroscopy section)
References
1) Chopra, K.L.
(1969). Thin film phenomena.
2) Fowles, G.R. (1975).
Introduction
to modern optics. 2nd
ed.
3) Hecht, E. (2002).
Optics. 4th ed.