AutocorrelationMeasuring a 100fs light pulse is no simple technical matter -- what reference can we use to measure a time so short that even light travels only 30 µm in that window? And then measure details within that small window? One way is to use the pulse: measure the pulse against itself. We can measure distances (which aren't so tiny here) and use the speed of light to convert those distances into time. This process is called autocorrelation.
You can easily imagine the simplest form: an interferometer. If the arms of the interferometer have equal pathlength, an interference pattern will result where the beams are recombined. If one arm is lengthened so that the pulses no longer overlap in time as they come together, the interference pattern will vanish. The distance needed to bring the copies of the pulse out of overlapping tells you the pulse duration of the pulse.
It isn't quite that simple, though, unless the pulse is transform-limited (like a carrier wave with a gaussian envelope). The inteference pattern made will vanish when the copies of the pulse are no longer coherent with each other, for distances greater than the coherence length of the pulses, and that can happen while the pulses still overlap.
A variation better than simple interferometry is to use a detector
that measures nonlinearly -- for instance, one that measures not
the intensity I but the square of the intensity. Then the signal
of an overlapping pulse will look something like 
,
while moving one arm by much more than a pulse's thickness will
make a non-overlapping signal 
.
So when the pulses overlap, the signal will be twice as large
as the background signal.
More precisely, pulses can partly overlap, and the signal will satisfy this formula:
where the intensity at the detector at any time depends on the intensity in each pulse, and the total signal integrates overthe whole time taken for the pulses to arrive. This is the formula for incoherent beams.
To be more precise, the intensity will come from the electric fields combining, and producing an intensity that may include interference. Therefore, the formula is more correctly:
When the two interferometer arms differ in length by half a wavelength, the two E fields will cancel, producing zero signal. Where they put the two copies of the pulse in phase, the E-field will be double, so the fourth power will give a signal 8 times the background signal. So as long as the pulses are coherent, there will be deep fringes that oscillate every wavelength of path-length difference. Eventually, as the pulses overlap but are not coherent, the signal will be twice the background; finally, for widely different arm-lengths, there will be only a constant-level background signal from two pulses uncorrelated with each other.
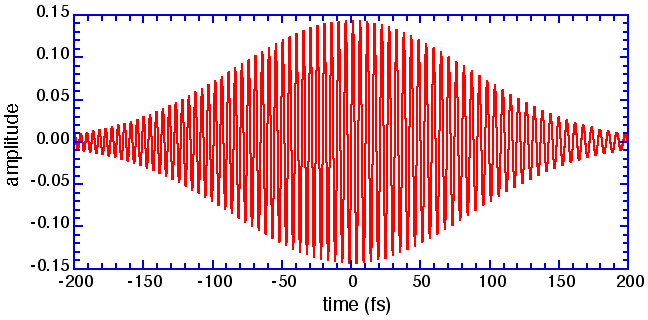
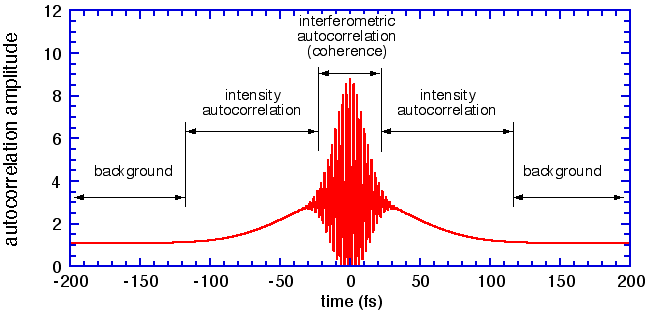
You can explore these differences, for short and long pulses, for transform-limited or chirped pulses, and for single or multiple pulses, using the interactive software Autocorrelation Illustration, which is available on the lab computer. This is the fastest way to get a feel for this material -- you'll see immediately the difference between the true pulse duration and the duration of that portion which is coherent, and has interference fringes.
There is a relation between the measured autocorrelation FWHM and the FWHM duration of the pulse (from the intensity envelope, not the E-field envelope).
tau-FWHM = K * t-FWHM
where for different intensity-envelope pulse types:
Pulse type
K value
gaussian
1.41
sech^2
1.55
from this, you can convert from the autocorrelation measurement
to infer a pulse duration. The pulse may not actually be either
of these two types, but ultrafast lasers are typically close to
a sech^2 form.
Last revised: 6 April 2003 - rsm
