USING THE FARADAY COMPUTER TO FIT GRAPHS

For many cases when you need to fit data to a function (linear, quadratic, etc.) the fitter in DataStudio you used in your first year labs is fine. However this fitter does not correctly include the effect of errors, and we recommend to use the far more sophisticated fitter on the main lab computer, Faraday. Instructions on how to access and use this fitter follow.  You may also want to check out the:

FARADAY Tutorial for fitting Polynomials

ENTERING YOUR DATA

1.Directly to Faraday

Click on the Faraday X terminal icon on the desktop (or log on to the computers in NORTEL lab or MP257. Follow the menu to find the item create ;  enter your data following the instructions (data goes in columns). Then you can go directly to the fitter (use the fit menu item).

2. From Excel

Suppose you  enter your data in Excel. The file must contain only numbers (no heading) with each variable in its own column - e.g. x, dx, y, dy . Save it as a .txt file (tab or space delimited) in the local computer you are using or in your directory in Faraday. If you want to name the variables (optional), create another .txt file with the variables in the same order as the data file, their names in the first row. Save this file, again in .txt format. Without  a variables file, Faraday will simply call the variables var1, var2, etc.

ACCESSING THE FARADAY FITTER

You can access Faraday's fitter by telnet from your home computer; click on Start on your desktop, type in telnet faraday.physics.utoronto.ca. Login to get the main menu. This is a good option if you want to massage your data before fitting.

If, however, all you want to do is fit the data, the access through the Web is more convenient (see below). Log on to the Web. Follow the links from the Department of Physics home page to UPSCALE, then to Data. In the "Data Analysis Tools" click on Linear Fit. You will be asked for your login name and password. Click on the appropriate link to find the file with your variable names (optional) and your data (use the Browse button to be sure of the file address!) then click on Submit. (N.B. a small bug in the program sometimes means that you will get an erroneous message telling you that the selected file contains no data. If that happens, click the RIGHT button on the mouse and select Open Frame in New Window on the pop-up menu.) The set-up window should then appear. When entering the data to the fitter, remember that whatever you want to go on the y-axis is called the Dependent Variable.

USING THE FARADAY FITTER

By default the Faraday fitter fits to a polynomial in the independent variable where the independent variable may be any legitimate math  expression involving the variables in addition to the simple variables you have entered. To use the fitter to fit to other linear models such as Fourier Series or Bessel Functions etc. see "Advanced Options" in the Fitter.

Fitting a Curve (Line) To Your Data The lab computer provides an "objective" procedure for giving a best fit of a straight line or a specified polynomial to your data, along with correctly calculated error estimates on that fit.  Basically the computer calculates the square of the distance between your data points and the curve it is trying to find; it then adjusts the constants of the polynomial representing the curve until the sum of these squares is a minimum. It gives you the values of the constants so found, along with their errors (one standard error). In addition it draws a graph which shows your data points and the fitted curve. If the errors in your data points are large enough to be visible on the graph, the computer also draws two lines which correspond to the "maximum" and "minimum" lines which would appear in a hand-drawn graph; however the computer's lines are correctly calculated to be ± one standard deviation from the fitted line. The graph itself is an important visual aid to determine the reasonableness of your fit. The program is menu-driven, and mostly self-explanatory. 

IN CASE YOU DID NOT HAVE A CHANCE TO USE THE FARADAY FITTER BEFORE  READ THE FOLLOWING TIPS

These tips will save you huge amounts of time!!

Your variable names should be short mnemonics, in lower case; e.g. s,t,vc etc., rather than distance, time, voltage (the less typing, the less chance of error; Mathematica functions start with an upper case letter).

Always enter your raw data, just as you have taken it (the computer will do any calculations on it that you need - see below).

As long as the errors on your data are either constants (e.g. 0.005, 0.3, etc.) or functions of the variables (e.g. 0.005/t², 2s/t, etc.) you do NOT need to enter them (you can enter them at the time of setting up the graph). Otherwise, however, you need to define a variable name for your errors and enter the numerical value for each point.

The fit window has a table which contains the variable names you have defined; alternatively it will provide the names var1 and var2. As far as the computer is concerned, the dependent variable will appear on the y-axis and the independent variable on the x-axis (these don’t necessarily have anything to do with which variable was dependent or independent in your actual experiment); make your own choice depending on how you want your final graph to look. You also need to define the errors in these quantities. If you want to plot the variables and errors just as they were defined, choose the appropriate "buttons"; if you want to manipulate the data somewhat (or, e.g. insert a constant value for an error) choose the button which reads An expression - you can then enter a constant value or a formula to calculate the variable you want to use.

Notes on calculations using Mathematica.

Some of the grammar you may need when you calculate mathematical expressions involving your variables is listed in the table opposite; (you can probably guess at any others you may need - see also "Mathematica", listed in References).

Algebraic Expression	Mathematica Expression
xy	x*y OR x  y (be safe -  use x*y)
1/x	1/x
x^n	x^n
Square root of x	Sqrt[x]
ln(x)	Log[x]
e^x	Exp[x]
log10(x)	Log[10,x]
cos(x)	Cos[x]
sin^-1(x)	ArcSin[x]
|x|	Abs[x]

N.B. Use "(" and ")" as parenthesis in your expressions; "[" and "]" are reserved for the arguments of Mathematica functions. Angles are measured in radians.

To all data, the computer fits a general polynomial which has the form:

y = A(0) + A(1)x + A(2)x² + A(3)x³ + ...

You need to specify which of the terms in the polynomial are relevant to the fit of your data; this is done by inserting the required powers (separated by commas or spaces) in the box provided or by selecting the appropriate "buttons" in the window from the set:

0	1	2	3	4	5	6	7	8		9
to choose one or more of the coefficients
A(0)	A(1)	A(2)	A(3)	A(4)	A(5)	A(6)	A(7)	A(8)	A(9)

(Often you will be specifying 0 and 1, which is a fit to the straight line y = A(0) + A(1)x with A(1) = slope and A(0) = intercept on the y axis). Follow the on-screen menu to try another fit, or re-plot the graph with a variety of options, or print the graph on the lab printer.

Other Useful Features of the Faraday Analysis Programs.

If you have entered your data directly into Faraday (see section above), the following features are available.

Note: When you use a menu item, you need usually type in only enough letters to uniquely identify the word; most of the time only the first letter is sufficient.

A) Once you have used create to enter your data, you can always look at it by choosing the menu item show which is available on the data and the analyse menus (the latter also gives you the option to print the data file).

B) There are several ways in which you can change your data after you have created it. You should almost never have to type in the full set of data again, since these programs will make almost all the corrections you want.

i) edit. This is the simplest of these programs, and should be used only for simple fixes. You can move around your data file, deleting, changing and adding data. To exit edit click on File (top left corner of the screen) to pull down the menu there. Choose the End option; you will then be prompted to Save before exiting. CAUTION! Occasionally you will get a message which reads Wrong columns or non-numbers found ; this often means that you have left the cursor sitting on a new line instead of exactly at the end of your data. Move the cursor to the end of the file and use the Backspace button to delete any extra spaces or line returns till the cursor is sitting immediately after the last digit of your last data point. Then try exiting again.

ii) massage. You will find this programs in the analyse menu. Clicking on massage will lead you to another menu with several options. The two which you will find most useful are now discussed.

recalc. This option presents you with the opportunity to add variables to your data set which are either constants or functions of the ones you have already defined. For example, in the Boyle’s Law experiment you may mistakenly have added mm of mercury (from the barometer reading) to cm of mercury (manometer reading), and all your pressure data has to be changed. Or you may have a very complicated expression to calculate from the raw data which you have entered in the file (the Flywheel experiment is a good example). You are asked how many new variables you want to define, their names, and how the computer is to calculate them from the data already in your file. NOTE! You are first asked if you want to keep the original data - it is usually a good idea to answer yes to this question.

addvar. You may decide that you want to add the values of a variable which you had forgotten to enter the first time. This option will ask you how many variables you want to add, and their names. It will present you, a line at a time, with the data that is already in your file. You just have to type in the new values. The programs will exit automatically when you reach the last line.

The Chi-Squared (χ²) test

Along with the fitted parameters, A(0), A(1), A(2) etc (let us call the number of these parameters m) a value called Chi-squared is printed at the top of your graph (the Greek symbol is χ, pronounced like “cry”, without the “r”). This is a statistical quantity which tells you something about the quality of your fit. (You will come across the quantity χ² in procedures in which averages are derived from data or in which curves are fitted to data, curve fitting being just another form of averaging.) For the case of the curve fitting described above, the value is calculated by taking the sum of the squares of the deviation of each of the n data points from the fitted curve and dividing by the square of the error (= standard deviation) in each point:

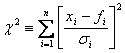
where x_i are the observed values, σ_i are the uncertainties in these values, and f_i are the predicted values based on your fitted parameters.

The size of χ² depends on how well the curve fits the data, taking into account the size of the actual error bars in your data. Its value will also depend on the number of terms in the sum, equal to the number of data points. For a good fit, we might expect that, on average, each point might deviate from the fitted curve by approximately the value of the stated error. Therefore, the sum would have a value approximately equal to the number of data points if the number of extracted parameters is small.

If we have overestimated the errors, χ² would be too low. If some of the points deviate from the fitted curve by more than we expect from the size of the errors, χ² will be too high. It can be shown that the expected value of χ² is ν, where ν =n-m is called the “degrees of freedom”. If your value of χ² differs greatly from ν, you should suspect the goodness of your fit to the data.

This qualitative understanding can be made quantitative; χ² has a statistical distribution which is well known. The calculated values in the χ² Distribution Table on the next page give the probability that, in a random process, that the given value of would be smaller than the value that you actually obtained. For example, if your χ² =23.21 for 10 degrees of freedom, then 99% of the time you would expect a smaller value of χ².

Percentile values for the χ² distribution with ν degrees of freedom.

ν	0.5%	1%	2.5%	5%	10%	90%	95%	97.5%	99%	99.5%
1	.00004	.00016	.00098	.0039	.0158	2.71	3.84	5.02	6.63	7.88
2	.0100	.0201	.0506	.1026	.2107	4.61	5.99	7.38	9.21	10.60
3	.0717	.115	.216	.352	.584	6.25	7.81	9.35	11.34	12.84
4	.207	.297	.484	.711	1.064	7.78	9.49	11.14	13.28	14.86
5	.412	.554	.831	1.15	1.61	9.24	11.07	12.83	15.09	16.75
6	.676	.872	1.24	1.64	2.20	10.64	12.59	14.45	16.81	18.55
7	.989	1.24	1.69	2.17	2.83	12.02	14.07	16.01	18.48	20.28
8	1.34	1.65	2.18	2.73	3.49	13.36	15.51	17.53	20.09	21.96
9	1.73	2.09	2.70	3.33	4.17	14.68	16.92	19.02	21.67	23.59
10	2.16	2.56	3.25	3.94	4.87	15.99	18.31	20.48	23.21	25.19
11	2.60	3.05	3.82	4.57	5.58	17.28	19.68	21.92	24.73	26.76
12	3.07	3.57	4.40	5.23	6.30	18.55	21.03	23.34	26.22	28.30
13	3.57	4.11	5.01	5.89	7.04	19.81	22.36	24.74	27.69	29.82
14	4.07	4.66	5.63	6.57	7.79	21.06	23.68	26.12	29.14	31.32
15	4.6	5.23	6.26	7.26	8.55	22.31	25	27.49	30.58	32.80
20	7.43	8.26	9.59	10.85	12.44	28.41	31.41	34.17	37.57	40.00
30	13.79	14.95	16.79	18.49	20.60	40.26	43.77	46.98	50.89	53.67
40	20.71	22.16	24.43	26.51	29.05	51.81	55.76	59.34	63.69	66.77
60	35.53	37.48	40.48	43.19	46.46	74.40	79.08	83.30	88.38	91.95
120	83.85	86.92	91.58	95.70	100.62	140.23	146.57	152.21	158.95	163.64

Confidence Levels

Suppose that the result of a measurement of some quantity x yields a result of x_m. We have already seen that this means there is a 68% chance that the mean of x lies between the values x-σ_m and x+σ_m and a 95% chance that it lies between the values of x-2σ_m and x+2σ_m. We could also say for example:

“With 99% confidence, the mean of x has a value lying between x-3σ_m and x+3σ_m.”

In the same way, the χ² test can give an idea of our confidence in a given result. If the value of the probability obtained from the χ² table is greater than 95%, then in only 5% of the random samples from the population in question would the value of be greater than the one actually found. We then say that our hypothesis (that the fit is a good one) is rejected at the 5% significance level and we should then consider our particular hypothesis regarding the data as suspect. Values at the 1% level of probability are said to be highly significant. Note that the χ² test is a negative test and only tells us if our hypothesis regarding the data is incorrect.

Examples: Suppose a fit gives a χ² of 4.2 for 6 degrees of freedom. The table shows us that this corresponds to a probability between 10% and 90%, which would be an acceptable fit. If the χ² was 16.81, then we should reject the fit at the 1% confidence level. Perhaps we have underestimated our errors or made a mistake in one or more of our measurements. If the χ² was 0.872, we would be concerned that the fit was “too good” and perhaps we had underestimated the error bars. Again, the fit is rejected at the 1% confidence level.