The relationship between determinism and randomness is fuzzier than it might first appear. Even perfectly deterministic classical systems may be chaotic. Chaos was first identified in classic situations like the Three Body Problem, but was not fully appreciated untill computers became widely available in the 1970s.
Chaos is characterized by sensitive dependence on initial conditions, a very common situation in even slightly complex mechanical systems like the double pendulum. This sensitivity is popularly known as the Butterfly Effect, and was made famous by the Jurassic Park movie.
Here is a great overall discussion of chaos. See also the first three chapters from the textbook, Deep Simplicity.
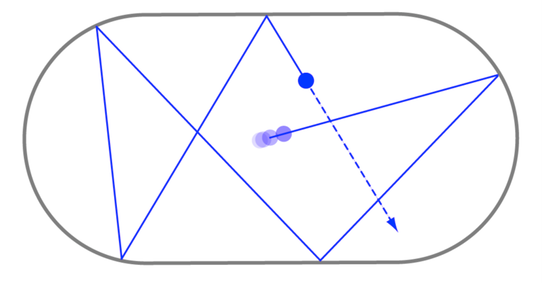
An even simpler situation is that of a Bunimovich Stadium --- an oddly shaped game of frictionless billiards. See a version that shows the sensitivity to initial conditions here. A simplified version of the Three Body Problem can be messed with here.
Ed Lorenz "discovered" chaos while working on a simple model of convection in the atmosphere. It is equivalent to a leaky waterwheel. You can see videos of these here, and here. A more professional discussion is here. Here is an app you can mess with.
Chaos produces effectively random trajectories, even though the underlying Newtonian equations are fully deterministic. Even the tiniest variation of the initial conditions is amplified until it takes over the motion, making long term prediction impossible. A similar problem, only much worse, makes long term weather prediction impossible.
There is a deep connection between chaos and fractals, which will be the next topic of the course. This is exemplified by the chaos game, a random procedure which nevertheless creates a weird sort of order. What emerges is a Sierpinski triangle. Why? Because this shape is an attractor --- the dynamics always approaches it and stays very close to it thereafter.
Physically, chaotic systems necessarily involve nonlinearity. A simple, but not very physical example is the Logistic Map, a sort of crude population model. Here is a site where you can look at the output of this model. Here is a zoomable picture of the bifurcation diagram of this map, which has a remarkable period doubling fractal tree structure.
Lorenz's theory of the atmosphere leads to something called the Lorenz model, whose 3D attractor is can be viewed and messed with here. Ironically, it looks like a butterfly! The three dimensional space that describes the space of this model is called its phase space. The phase spaces of more complex systems, like the double pendulum or the atmosphere, are higher dimensional.
Certainly the most famous fractal is the Mandelbrot set. "Mandel diving" is a geeky way to spend an afternoon. With enough computer power, you can dive very deep. Once you have done that, better eat your fractal vegetables. Or just watch the movie. Phyllotaxis, the process by which plants develop their arrangements of leaves and petals, has close connections with the Fibbonacci numbers and the mysterious Golden ratio. Sometimes, phyllotaxis produces fractal objects, but usually not.
Chaos and fractals seem to represent a new kind of order hiding behind the appearance of randomness. Extended to random fractals, such order becomes quite ubiquitous. Emergent fractal order appears in mundane things like dripping faucets and the shapes of trees.
Tablet notes: [ Lec 14 ] [ Lec 15 ] [ Lec 16 ]