notes

Open and closed systems, phase transitions

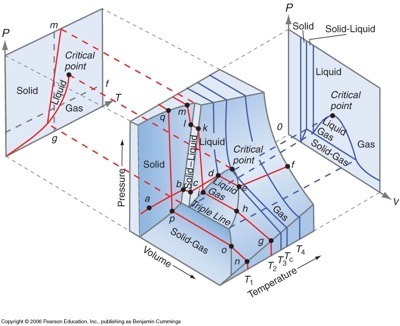Collections of identical atoms can behave in macroscopically different ways when their temperature and density are changed.  For example, water exists as a gas, a liquid and a solid at different temperatures.  Why?  These "phases" are collective effects that emerge under equilibrium conditions.  The changes, called "phase transitions", are a big object of study in Physics.  Changes of temperature in the early universe at which new collective modes of motion emerged, like the symmetry breaking in the standard model, are also usually called phase transitions.  Closed systems typically quickly reach thermodynamic equilibrium, after which nothing changes.  Equilibrium can usually be assumed if the external conditions on a closed system are changed slowly enough.  Open systems, on the other hand, are generally under non-equilibrium conditions.

The distinction between open and closed systems in crucial to the Second Law because open systems do not have to have increasing entropy.  The Earth is an open system: it receives energy from the sun and exports an equal amount of energy to the cold night sky.  The whole biosphere copiously produces entropy all the time, but this does not mean that the entropy of the biosphere must increase, because it is not open.  For a more technical discussion, see here. (Many foolish people believe that biological evolution contradicts the Second Law --- there are many web pages about this -- but this is completely incorrect).

The Ising model of a magnetic phase transition.  Here we see how a new ordered structure can spontaneously emerge as some external parameter (here the temperature) is varied continuously.  The transition point, often called a critical point, is sharp and the new phase can appear continuously or discontinuously at that "tipping point".  At lot has been written about such points, including much nonsense.  Near a critical point, fluctuations can become very large as the system becomes "soft" at the transition.  Such points are more generally called bifurcation points and they can occur in non-equilibrium systems as well, and can lead to the sudden appearance of new states of motion or even spatial patterns.  A good example is the onset of period 2 in the logistic map.  Pattern formation is the study of such non-equilibrium structures.


Tablet notes: (Lec 18 -- no notes) [ Lec 19 ] [Lec 20 ][ Lec 21 ][ patterns ]

Nov 23, 2011 2:41 PM

The arrow of time, irreversibility and the second law of thermodynamics

Why is the future different than the past? What accounts for the persistence of memory? The microscopic laws of physics are time reversible, a fact which is closely associated with the conservation of energy, a deep universal law.  Yet we observe a real difference between the past, which stretches back to the Big Bang, and the future which seems as-yet unformed, subject to change and even free will.  Why?

Part of the physical explanation of this The Arrow of Time comes from the distinction between macrostates and microstates.  Macroscopic systems involve a lot of fundamental particles and have new properties like temperature that individual particles do not.  The 19th century science of steam engines, thermodynamics, plus the modern theory of statistical mechanics, worked out by James Clerk Maxwell, J. Willard Gibbs and Ludwig Boltzmann, explains the difference statistically.  The motion of complex systems might reverse, but it is extremely unlikely.  This is encoded in the Second Law of Thermodynamics, which states that Entropy in a closed system must always increase or stay constant.  The three laws of thermodynamics were memorably recited in a song by Flanders and Swan. C. P. Snow also chimed in regarding the Second Law and the Two Cultures.

The Arrow of Time also has cosmological, psychological and quantum mechanical manifestations.  But even if we manage to figure out why time has a direction, we are still left with the problem of explaining the Present.  The current moment of time, although fleeting, seems different than either the past or the future.  This appears to be a problem for which physics has no explanation at all, as it seems to involve the nature of consciousness etc. Consciousness is perhaps the greatest mystery of emergence.  


Tablet notes: [ Lec 17 ]

Nov 16, 2011 11:04 AM

Introduction to chaos

The relationship between determinism and randomness is fuzzier than it might first appear.  Even perfectly deterministic classical systems may be chaotic.  Chaos was first identified in classic situations like the Three Body Problem, but was not fully appreciated untill computers became widely available in the 1970s.

Chaos is characterized by sensitive dependence on initial conditions, a very common situation in even slightly complex mechanical systems like the double pendulum.  This sensitivity is popularly known as the Butterfly Effect, and was made famous by the Jurassic Park movie.

Here is a great overall discussion of chaos.  See also the first three chapters from the textbook, Deep Simplicity.

An even simpler situation is that of a Bunimovich Stadium --- an oddly shaped game of frictionless billiards.  See a version that shows the sensitivity to initial conditions here.  A simplified version of the Three Body Problem can be messed with here.

Ed Lorenz "discovered" chaos while working on a simple model of convection in the atmosphere.  It is equivalent to a leaky waterwheel.  You can see videos of these here, and here. A more professional discussion is here. Here is an app you can mess with.

Chaos produces effectively random trajectories, even though the underlying Newtonian equations are fully deterministic.  Even the tiniest variation of the initial conditions is amplified until it takes over the motion, making long term prediction impossible.  A similar problem, only much worse, makes long term weather prediction impossible.

There is a deep connection between chaos and fractals, which will be the next topic of the course.  This is exemplified by the chaos game, a random procedure which nevertheless creates a weird sort of order.  What emerges is a Sierpinski triangle.  Why?  Because this shape is an attractor --- the dynamics always approaches it and stays very close to it thereafter.

Physically, chaotic systems necessarily involve nonlinearity. A simple, but not very physical example is the Logistic Map, a sort of crude population model.  Here is a site where you can look at the output of this model.  Here is a zoomable picture of the bifurcation diagram of this map, which has a remarkable period doubling fractal tree structure.

Lorenz's theory of the atmosphere leads to something called the Lorenz model, whose 3D attractor is can be viewed and messed with here.  Ironically, it looks like a butterfly!  The three dimensional space that describes the space of this model is called its phase space.  The phase spaces of more complex systems, like the double pendulum or the atmosphere, are higher dimensional.

Certainly the most famous fractal is the Mandelbrot set.  "Mandel diving" is a geeky way to spend an afternoon.  With enough computer power, you can dive very deep.  Once you have done that, better eat your fractal vegetables. Or just watch the movie. Phyllotaxis, the process by which plants develop their arrangements of leaves and petals, has close connections with the Fibbonacci numbers and the mysterious Golden ratio.  Sometimes, phyllotaxis produces fractal objects, but usually not.

Chaos and fractals seem to represent a new kind of order hiding behind the appearance of randomness.  Extended to random fractals, such order becomes quite ubiquitous.  Emergent fractal order appears in mundane things like dripping faucets and the shapes of trees.


Tablet notes: [ Lec 14 ] [ Lec 15 ] [ Lec 16 ]


Nov 1, 2011 4:19 PM