In this talk I will discuss the general theoretical framework of estimating potential-field signals and their power-spectral densities from noisy and incomplete data distributed on the surface of a sphere - at an altitude above the source. This class of statistical inverse problems is of great importance in geodesy, geophysics and planetary physics, but also in computer science, cosmology, and medical imaging. The key innovation is the development of spatio-spectrally concentrated spherical basis functions which draw on the work of Slepian and Shannon, and of a very general statistical framework for their application. Our examples are geophysical in nature. The first example is concerned with estimating the diminishing ice mass over Greenland from time-variable GRACE-satellite gravity. The second set of examples is on using satellite gravity to study the source signature of large earthquakes. As a third and final example I study the distribution of crustal magnetization on Mars and Earth from satellite measurements of their magnetic fields.

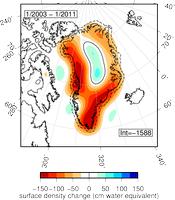
Simons: Total Mass Map