Over the last 30 years the standard model of particle physics has gradually taken shape. The standard model has withstood tests of unprecedented precision. Still, we know that this model cannot be complete. Experimentalists and theorists at the University of Toronto are actively trying to find ways to move beyond the current particle physics paradigm.Our group is involved in the ATLAS experiment at CERN, near Geneva Switzerland, studying the highest energy man-made proton proton collisions, the T2K experiment in Japan, which studies long baseline neutrino interactions, and the SuperCDMS experiment at SNOLAB, which searches for dark matter.
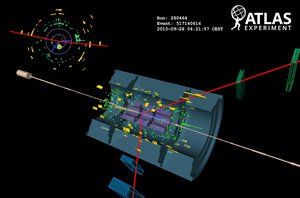
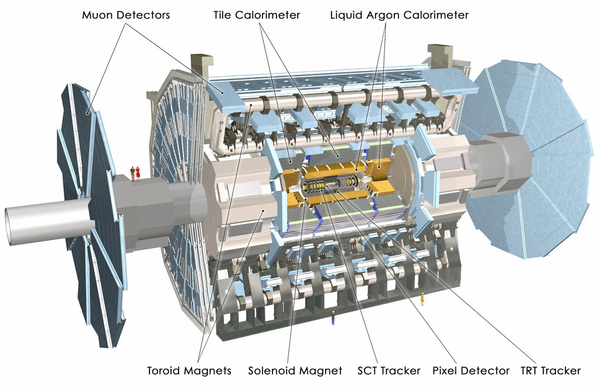
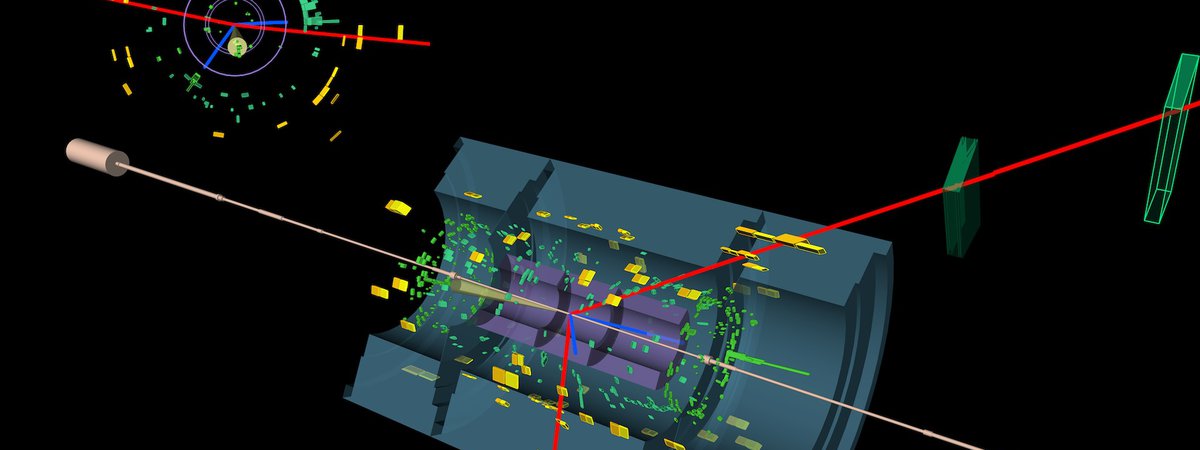
The LHC came into operation at CERN in 2010, and now defines the "energy frontier" where we can study the highest energy particle interactions made in the laboratory. Our experimental group plays a leading role in the scientific studies, maintenance, operations and potential upgrades of the ATLAS experiment. We were involved in the 2012 discovery of the Higgs boson, which gives rise to the mass of all of the fundamental particles in the Standard Model of particle physics. We are now engaged in detailed studies of the Higgs boson and the top quark, as well as in searches for new particles that will lead us to a deeper understanding of how our universe is structured. In addition to our physics studies, we continue to maintain the ATLAS forward calorimeter, that was partially assembled on campus in Toronto and we are actively involved in building over 1000 silicon tracker modules for the ATLAS tracker upgrade that will be installed, at CERN, in the second half of this decade.
While ATLAS is uncovering the origin of mass, the T2K experiment is investigating the deep mystery why the mass we see in our universe in galaxies, stars and us is only matter, with no anti-matter component. The solution may be in an asymmetry between neutrinos and anti-neutrinos, which T2K is studying. The Toronto group is active in the neutrino beam instrumentation and the neutrino mixing angle physics analysis.
We have convincing astrophysical evidence that approximately a quarter of the universe consists of dark matter, which is thought to be outside the standard model. The SuperCDMS (Cryogenic Dark Matter Search) experiment looks for interactions of dark matter particles in silicon and germanium crystal detectors. SuperCDMS operated in an underground laboratory in Minnesota until 2015; now, the collaboration is building an even more powerful version of the experiment in SNOLAB, Canada's world-leading astroparticle physics facility. Construction is currently underway, with first operations expected in 2021 and a test facility opening even sooner. Our group focuses mostly on data acquisition and analysis; members also make trips to SNOLAB for commissioning and operations shifts.
All three of these experiments provide a number of exciting opportunities for graduate research into new particle physics phenomena at either the M.Sc. or Ph.D. level, with the possibility of gaining essential instrumentation and hardware experience working on upgrades for ATLAS. More information on the opportunities for graduate students in our groups can be found here .