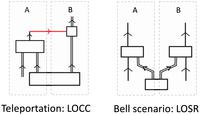A standard approach to quantifying resources is to determine which operations on the resources are freely available and to deduce the ordering relation among the resources that these operations induce. If the resource of interest is the nonclassicality of the correlations embodied in a quantum state, that is, entanglement, then it is typically presumed that the appropriate choice of free operations is local operations and classical communication (LOCC). We here argue that, in spite of the near-universal endorsement of the LOCC paradigm by the quantum information community, this is the wrong choice for one of the most prominent applications of entanglement theory, namely, the study of Bell scenarios. The nonclassicality of correlations in such scenarios, we argue, should be quantified instead by local operations and shared randomness (LOSR). We support this thesis by showing that various perverse features of the interplay between entanglement and nonlocality are merely an artifact of the use of LOCC-entanglement and that the interplay between LOSR-entanglement and nonlocality is natural and intuitive. Specifically, we show that the LOSR paradigm (i) provides a resolution of the "anomaly of nonlocality", wherein partially entangled states exhibit more nonlocality than maximally entangled states, (ii) entails a notion of genuine multipartite entanglement that is distinct from the conventional one and which is free of several of its pathological features, and (iii) makes possible a resource-theoretic account of the self-testing of entangled states which simplifies and generalizes prior results. Along the way, we derive some fundamental results concerning the necessary and sufficient conditions for convertibility between pure entangled states under LOSR and highlight some of their consequences, such as the impossibility of catalysis for bipartite pure states.

Video of the talk: My Media Link